PARALLELOGRAMMES ET
PARALLELOGRAMMES
PARTICULIERS 		 
     

I. Parrallélogrammes.

 
Définition :
 
  Un parallélogramme est un quadrilatère dont tous ses côtés opposés sont parallèles deux à deux.
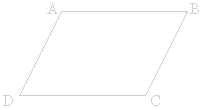(AB) // (CD)
et
(AC) // (BD)

 
Propriété :
 
  Si un quadrilatère a ses côtés opposés de même longueur alors c'est un parallélogramme.
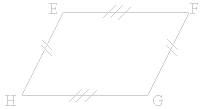EF = GH
et
EH = FG

 
Propriété :
 
  Si un quadrilatère a deux de ses côtés opposés de même longueur et parallèles alors c'est un parallélogramme.

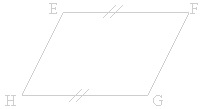EF = GH
et
(EF) // (GH)

 
Propriété :
 
  Si un quadrilatère est un parallélogramme alors il a tous ses côtés opposés de même longueur et parallèles.

 
Propriété :
 
  Si un quadrilatère a ses angles opposés de même mesure alors c'est un parallélogramme.

 
Propriété :
 
  Si un quadrilatère est un parallélogramme alors tous ses angles ont même mesure.
LIJ = JKL
et    
IJK = KLI

 
Propriété :
 
  Si un quadrilatère a ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme.
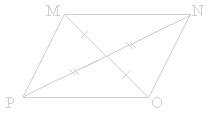MI = IO
et
NI = IP

  Remarques : L'intersection des diagonales est le centre de symétrie du parallélogramme.

 
Propriété :
 
  Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur milieu.

II. Losanges.

  Remarques : Un losange est un parallélogramme particulier alors toutes les propriétés du parallélogramme restent vraies pour le losange.

 
Définition :
 
  Un losange est un quadrilatère dont tous ses côtés ont la même longueur.
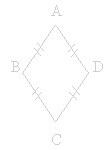AB = BC = CD = DA

  Remarques : En général pour prouver qu'un quadrilatère est un losange, on montre d'abord que c'est un parallélogramme puis on utilise l'une des propriétés suivantes :

 
Propriété :
 
  Si un parallélogramme a deux côtés consécutifs de même longueur alors c'est un losange.

 
Propriété :
 
  Si un parallélogramme a ses diagonales perpendiculaires alors c'est un losange.
(EG)   (FH)

 
Propriété :
 
  Si un quadrilatère est un losange alors il a ses quatre côtés de même longueur, ses côtés opposés parallèles, ses diagonales perpendiculaires et qui se coupent en leur milieu.

III. Rectangles.

  Remarques : Un rectangle est un parallélogramme particulier alors toutes les propriétés du parallélogramme restent vraies pour le rectangle.

 
Définition :
 
  Un rectangle est un quadrilatère avec quatre angles droits.
(AB)   (BC)
(BC)   (CD)
(CD)   (AD)
(AD)   (AB)

  Remarques : En général pour prouver qu'un quadrilatère est un rectangle, on montre d'abord que c'est un parallélogramme puis on utilise l'une des propriétés suivantes :

 
Propriété :
 
  Si un parallélogramme a un angle droit alors c'est un rectangle.

 
Propriété :
 
  Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.
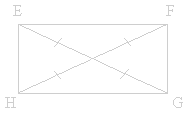EG = FH

 
Propriété :
 
  Si un quadrilatère est un rectangle alors il a ses côtés opposés parallèles et de même longueur, ses angles opposés de même mesure, quatre angles droits, ses diagonales de même longueur qui se coupent en leur milieu.

IV. Carrés.

  Remarques : Un carré est un parallélogramme particulier alors toutes les propriétés du parallélogramme restent vraies pour le carré.

 
Définition :
 
  Un carré est un quadrilatère qui est à la fois un losange et un rectangle.
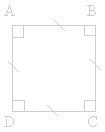AB = BC = CD = DA
(AB)   (BC)
(BC)   (CD)
(CD)   (AD)
(AD)   (AB)

  Remarques : En général pour prouver qu'un quadrilatère est un carré, on montre d'abord que c'est un parallélogramme puis on utilise l'une des propriétés suivantes :

 
Propriété :
 
  Si un losange a un angle droit alors c'est un carré.

 
Propriété :
 
  Si un losange à ses diagonales de même longueur alors c'est un carré.

 
Propriété :
 
  Si un rectangle a deux côtés consécutifs de même longueur alors c'est un carré.

 
Propriété :
 
  Si un rectangle a ses diagonales perpendiculaires alors c'est un carré.

 
Propriété :
 
 
Si un quadrilatère est un carré alors il a quatre côtés de même longueur, ses côtés opposés parallèles, quatre angles droits, ses diagonales de même longueur qui se coupent en leur milieu et perpendiculairement.

V. Résumé.


 

 Quadrilatère









* Les côtés opposés sont parallèles
* Les côtés opposés sont de même longueur		  







* Les diagonales se coupent en leur milieu
* Les angles opposés sont de même mesure



  Parallélogramme






* Les diagonales ont même longueur
* Il y a un angle droit		  
* Deux côtés consécutifs de même longueur
* Les diagonales sont perpendiculaires


Rectangle   Losange











* Deux côtés consécutifs de même
longueur

* Les diagonales sont perpendiculaires 		 

* Il y a un angle droit

* Les diagonales ont même
longueur


Carré