| |
|
| |
|
|
| |
REPERAGE
ET
COMPARAISON
DES RELATIFS |
|
| |
|
|
| |
|
|
Sur
une droite graduée, on appelle abscisse d'un point
la distance le séparant de l'origine. |
| |
|
|

A a pour abscisse -3 et B a pour abscisse 4. |
| |
|
|
On
appelle repère du plan, deux droites graduées
perpendiculaires de même origine. |
| |
|
|
On
appelle abscisse d'un point dans un repère la distance
le séparant de l'origine sur l'axe horizontal appelé
axe des abscisses. |
| |
|
|
On
appelle ordonnée d'un point dans un repère la
distance le séparant de l'origine sur l'axe vertical
appelé axe des ordonnées. |
| |
|
|
On
appelle coordonnées d'un point dans un repère,
l'ensemble des abscisses et des ordonnées repérant
le point. |
| |
|
|
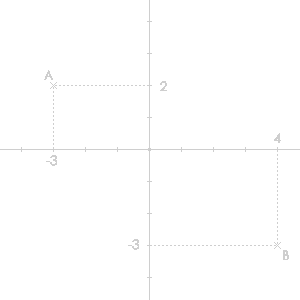
A a pour abscisse -3 et pour ordonnée 2 donc a pour
coordonnées (-3 ; 2)
B a pour abscisse 4 et pour ordonnée -3 donc a pour
coordonnées (4 ; -3) |
| |
|
|
On note toujours en premier l'abscisse suivie
de l'ordonnée pour les coordonnées :
|
|
II. Comparaison.
| |
|
|
*
Pour comparer deux nombres positifs : le plus grand est le
plus éloigné de zéro.
* Pour comparer deux
nombres de signes différents : le plus grand est le
nombre positif.
* Pour comparer deux
nombres négatifs : le plus grand est le plus proche
de zéro. |
|
|
|