Angles

I. Vocabulaire.

Définition :

Un angle est formé par deux demi-droites de même origine.

Définition :

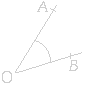
L'origine commune des deux demi-droites formant l'angle est appelée sommet de l'angle.

Exemple :

En angle est généralement noté avec trois points : Le point central est le sommet de l'angle et les deux autres points sont des points de chaque demi-droites formant l'angle.
L'angle de la définition se note	AOB	.

Définition :

Un angle nul est un angle formé par deux demi-droites confondues.

Définition :

Un angle droit est formé par deux demi-droites perpendiculaires.

Définition :

Un angle plat est un angle formé par deux demi-droites alignées et non confondues.

Définition :

Un angle obtus est un angle compris entre un angle nul et un angle droit.

Définition :

Un angle aigu est un angle supérieur à un angle droit.

Exemple :

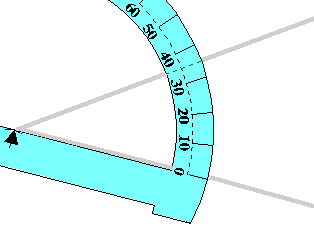
II. Rapporteur et mesures d'angles.

Méthode :

1. On place le rapporteur de telle façon que :	- son centre soit sur le sommet de l'angle.
	- le zéro de la graduation soit sur l'une des deux demi-droites.
2. On lit la mesure de l'angle à l'aide de la deuxième demi-droite.

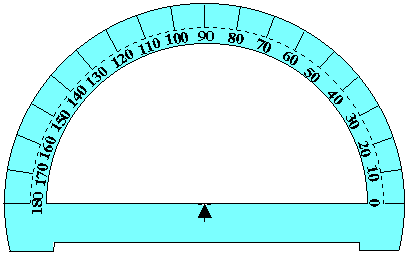Comment tracer un angle de 55° ?

Méthode :

1. On choisit un point comme sommet par exemple O.
2. On trace une demi-droite d'origine O passant par A.
3. On place le rapporteur de telle façon que	- son centre soit sur le sommet O. - le zéro de la graduation soit sur la demi-droite [OA).
4. On marque un point B qui correspond à la graduation de 55°.
5. On trace la demi-droite [OB).
6. On codifie la figure.

Propriété :

Si un angle est

- nul alors il mesure 0°.
- droit alors il mesure 90°.
- plat alors il mesure 180°.

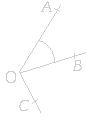
III. Bissectrice.

Définition :

La bissectrice d'un angle est son axe de symétrie.

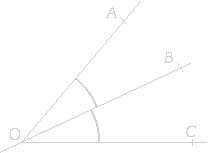Exemple :

bissectrice de

AOB

BOC