POURCENTAGES ET RELEVES STATISTIQUES

I. Pourcentages.

Définition :

Calculer un pourcentage d'un nombre revient à multiplier ce nombre par le taux de pourcentage issu de la proportionnalité.

Exemple :

Dire qu'un gâteau contient 15% de cacao signifie que la masse de cacao est proportionnelle à la masse du gâteau et que pour 100 grammes de gâteau, il y a 15 grammes de cacao. Masse de gâteau 50 100 200 500 1000 Masse de cacao 7,5 15 30 75 150 x 15   100 Calcul de la masse de cacao pour un gâteau de 120 grammes : 15% de 120 revient à calculer 15 x 120 100 15 x 120 = 0,15 x 120 = 18 100 Ainsi dans le gâteau qui pèse 120 grammes il y a 18 grammes de cacao.

II. Diagrammes.

1. Classement de données.

Dans un parking de 300 places, on a relevé les marques des voitures. 105 Renault, 90 Peugeot, 75 Citroën et 30 d'autres marques.

Marque Renault Peugeot Citroën Autres Total Nombre 105 90 75 30 300 Pourcentage 35 30 25 10 100
		x	1
			3

2. Diagrammes en barres.

Définition :

Un diagramme en barres (en bâtons) est constitué de rectangles (de segments) dont la longueur est proportionnelle aux pourcentages.

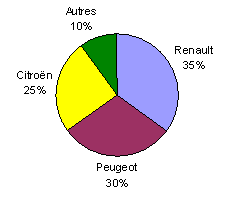
3. Diagrammes circulaires.

Définition :

Un diagramme circulaire (semi-circulaire) est constitué d'un disque (demi disque) partagé en secteurs. Les mesures des angles des secteurs sont proportionnelles aux pourcentages.

Exemple :

Pour calculer l'angle représenté par la marque Renault dans un diagramme circulaire (semi-circulaire), on doit calculer les 35% de 360° (de 180°). 35 x 360 = 126° 100 35 x 180 = 63 ° 100 .